A teoria moderna de portfólio é amplamente utilizada no mundo das finanças. Neste artigo, examinaremos mais de perto o que é a teoria moderna de portfólio, revisaremos um exemplo de cálculo e discutiremos as suposições por trás da teoria.
O que é a teoria moderna do portfólio?
A moderna teoria de portfólio (MPT) é amplamente utilizada em finanças e imóveis comerciais criar carteiras de investimento que maximizem o retorno para um determinado nível de risco ou, alternativamente, minimizem o risco para um determinado nível de retorno.
Harry Markowitz é conhecido como o pai da Teoria Moderna do Portfólio (MPT). Em 1952, ao completar sua dissertação de doutorado em economia na Universidade de Chicago, Harry Markowitz publicou uma parte de seu pesquisar em “Seleção de Portfólio” no Jornal de Finanças. Esta publicação marcou o início de uma nova linha de pesquisa em economia financeira e investimentos. Em 1990, Harry Markowitz recebeu o Prêmio Nobel de Economia por seu trabalho sobre a Teoria Moderna do Portfólio. Seu trabalho lançou as bases de como pensamos hoje sobre as decisões de investimento.
Utilizando o MPT, os investidores não consideraram apenas as características de risco e retorno dos ativos individuais, mas também as relações entre os retornos dos ativos. A chave do MPT é a ideia de benefícios de diversificação. Por outras palavras, os investidores devem considerar uma combinação óptima de diferentes activos para alcançar o retorno máximo para o nível de risco preferido do investidor.
Fundamentos da Teoria Moderna do Portfólio
De acordo com o MPT, os investidores não devem considerar os investimentos individuais apenas, mas como parte de uma carteira de activos. Esta carteira de ativos deve ser construída de forma a maximizar o retorno para um determinado nível de risco. Os investidores também podem reduzir o risco global da sua carteira, diversificando as suas participações através de activos individuais e não relacionados. Assim, os investidores devem considerar o impacto nas características de média-variância da carteira ao avaliar qualquer novo investimento. Usando o MPT, as duas características mais importantes de um ativo são o retorno esperado do ativo (média) e o desvio padrão dos retornos (variância).
Suposições da Teoria Moderna do Portfólio
A teoria moderna do portfólio pressupõe que os investidores são avessos ao risco. Isso não significa que os investidores não assumirão riscos, mas preferem riscos mais baixos a riscos mais elevados. Por exemplo, se dois investimentos rendem 10% cada, mas têm desvio padrão nesses retornos de 4% e 2%, o investidor avesso ao risco preferiria o ativo com variação de retorno de 2%.
Os investidores avessos ao risco também exigem um prémio por assumirem mais riscos. Portanto, os ativos com maior variância nos seus retornos devem compensar os investidores com retornos esperados mais elevados. Os investidores avessos ao risco também preferirão o ativo com o maior retorno esperado para um determinado nível de risco. Por exemplo, se você tiver dois ativos com desvio padrão de retorno de 4%, mas retorno esperado de 7% e 9%, o investidor avesso ao risco escolheria o ativo com retorno esperado de 9%.
A diversificação permite que um investidor reduza o risco geral da carteira e, ao mesmo tempo, atinja a taxa de retorno exigida pelo investidor sobre a carteira. Embora a diversificação não possa reduzir o risco sistemático (risco associado ao mercado financeiro global), pode reduzir o que é conhecido como risco idiossincrático. O risco idiossincrático de um ativo é uma medida da variação no retorno atribuído a essa ação específica. Isto difere do risco sistemático associado a todos os investimentos num mercado com resultados incertos. A diversificação não pode reduzir a exposição de um investidor ao risco sistemático.
Em última análise, é a correlação entre as distribuições de retorno dos activos que proporciona benefícios de diversificação. Se dois ativos tiverem uma correlação de 1,0, isso significa que eles têm aproximadamente a mesma distribuição de retorno. Se um ativo aumentar 2%, o outro também deverá aumentar 2%. Por outro lado, dois ativos com correlação de -1,0 têm distribuição de retorno exatamente oposta. Se um ativo aumentar 2%, o outro deverá diminuir 2%.
Teoria Moderna do Portfólio e A Fronteira Eficiente
Representar graficamente o desvio padrão e o retorno esperado (risco e retorno) para todas as carteiras possíveis produz uma imagem como a abaixo.
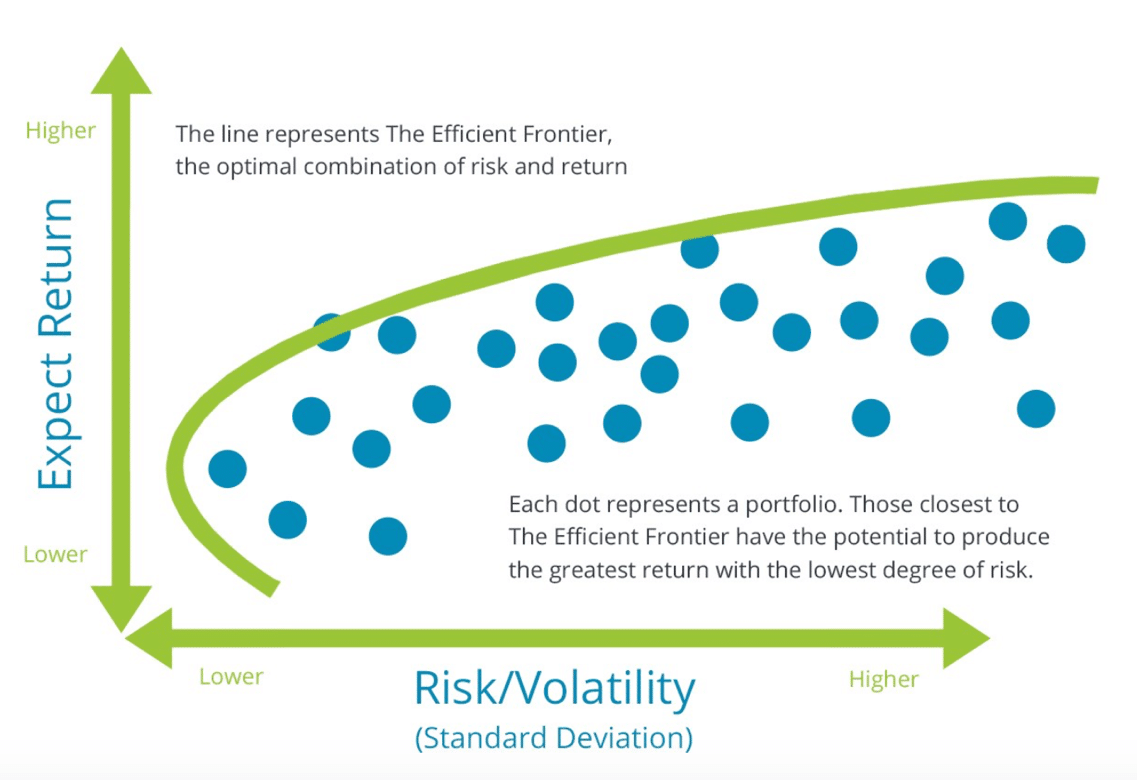
Dado que um investidor racional e avesso ao risco deve sempre escolher a carteira com o maior retorno esperado para um nível específico de risco, o gráfico de dispersão de todas as carteiras ilustra uma linha que é conhecida como fronteira eficiente. Os investimentos ao longo da fronteira eficiente proporcionam aos investidores o maior retorno esperado para um determinado nível de risco. Todas as carteiras que não estão localizadas ao longo da fronteira eficiente são subótimas. A fronteira eficiente demonstra o poder da diversificação porque contém uma variedade de carteiras que incorporam numerosos investimentos de diferentes maneiras.
Cálculos de exemplo da teoria moderna do portfólio
Para ver como isso funciona, comece com dois ativos que terão cada um um peso de 50% em uma carteira. A propriedade A tem um retorno esperado de 12% ao ano e um desvio padrão de 10% dos retornos. A propriedade B tem um retorno esperado de 9% ao ano e um desvio padrão de 8% dos retornos. A compensação risco-retorno exigida pelos investidores avessos ao risco mostra que são esperados retornos esperados mais elevados com maior risco de retornos. A correlação de retornos é de 0,4.
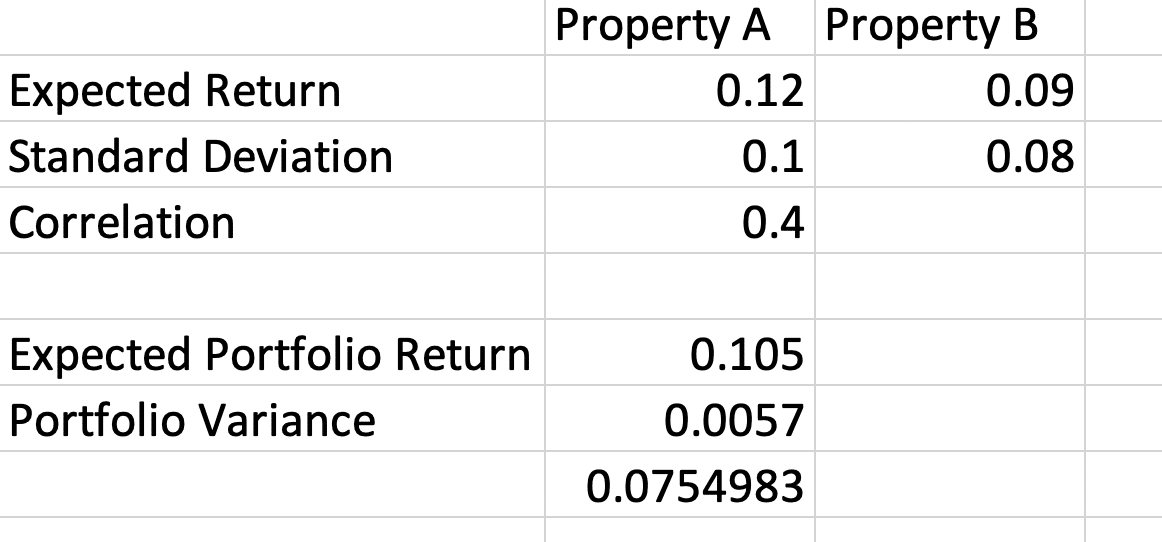
Para calcular o retorno esperado da carteira, encontre a média ponderada dos retornos dos dois ativos.
Retorno esperado do portfólio = (0,5)(0,12) + (0,5)(0,09) = 0,105 ou 10,5% ao ano
A fórmula para variação do portfólio é:
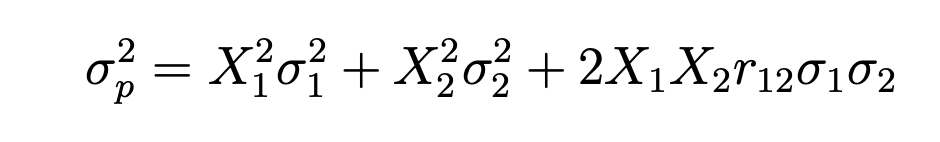
X1 = peso do ativo 1
σ1 = desvio padrão do ativo 1
X2 = peso do ativo 2
σ2 = desvio padrão do ativo 2
r12 = coeficiente de correlação dos ativos 1 e 2
Portanto, neste exemplo, o cálculo da variação da carteira seria:
Variância do portfólio = (0,52)(0,12) + (0,52)(0,092) + (2)(0,5)(0,5)(0,4)(0,1)(0,09) = 0,0057
Tirar a raiz quadrada da variância do portfólio resulta em um desvio padrão do portfólio de 0,075 ou 7,5% ao ano.
Portanto, este exemplo mostra o benefício da diversificação de carteiras de acordo com a teoria moderna de carteiras. A carteira de ativos apresenta risco menor (desvio padrão) do que qualquer um dos dois ativos isoladamente. A carteira também obtém um retorno mais elevado para um nível de risco mais baixo do que a Propriedade B neste exemplo.
Teoria Pós-Moderna do Portfólio
Os desenvolvedores de software Brian Rom e Kathleen Ferguson introduziram o conceito de Post Modern Portfolio Theory (PMPT) em uma publicação de 1993 no Revista de Gestão de Desempenho. O PMPT é essencialmente uma extensão da Teoria Moderna do Portfólio de Markowitz porque mantém a compensação entre risco e retorno em seu núcleo. A definição de risco é a principal diferença entre as duas teorias. A Teoria Moderna do Portfólio define o risco como o desvio padrão dos retornos, e os retornos positivos e negativos são ponderados igualmente. Por outro lado, o PMPT reconhece que os investidores estão muito mais preocupados com o risco negativo de um investimento. Por outras palavras, os investidores preocupam-se mais em perder dinheiro do que em ganhar mais dinheiro do que esperavam. Assim, o PMPT concentra-se inteiramente na componente negativa da distribuição de retorno no seu cálculo de risco.
Conclusões
A Teoria Moderna de Portfólio ainda constitui a base para a gestão de investimentos e seleção de portfólio. Os investidores procuram maximizar o seu retorno para um determinado nível de risco. Eles também usam a diversificação entre setores e classes de ativos para alcançar o equilíbrio mais eficiente do portfólio entre risco e retorno. Embora novas teorias e modelos refinem as tendências comportamentais com novas tecnologias, não nos afastamos muito da teoria original de Markowitz.
